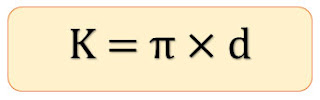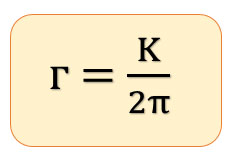Soal Pecahan Kelas 6 Kurikulum 2013 dan Pembahasan

Halo adik-adik, berikut adalah soal pecahan untuk kelas 6 kurikulum 2013 berupa kuis online yang mana kalian bisa langsung menjawab soal dengan cara mengklik bulatan di depan jawaban yang kalian anggap paling benar. Nilai/skor untuk setiap jawaban terpilih akan langsung ditampilkan otomatis. Skor untuk satu soal adalah 5. Total skor jika semua jawaban benar adalah 100.

Materi soal pecahan kelas 6 :

A. Menyederhanakan Pecahan

B. Mengubah Bentuk Pecahan

C. Mengurutkan Berbagai Bentuk Pecahan

Sebelum mengerjakan, mari kita pelajari dulu materi soal pecahan yang sudah disebutkan. Ulasannya ada di bawah. ini. 

Menyederhanakan Pecahan

Pecahan biasa adalah bentuk pecahan $\frac{a}{b}$ artinya a dibagi b. Di mana a merupakan pembilang dan b merupakan penyebut. Pecahan berbeda dapat bernilai sama.  Pecahan berbeda bernilai sama disebut pecahan senilai.

Contoh pecahan senilai :

$\frac{1}{2}$ = $\frac{2}{4}$ = $\frac{3}{6}$ = $\frac{4}{8}$

Bentuk pecahan dikatakan paling sederhana jika pembilang dan penyebut tidak memiliki faktor sekutu. Cara menyederhanakan pecahan adalah dengan membagi pembilang dan penyebut dengan bilangan yang sama (FPB)

Contoh :

Pecahan paling sederhana dari $\frac{30}{75}$ adalah ....

Jawaban :

FPB dari 30 dan 75 adalah 15

$\frac{30}{75}$ = $\frac{\textrm{30 : 15}}{\textrm{75 : 15}}$ = $\frac{2}{5}$

Jadi, bentuk pecahan paling sederhana dari $\frac{30}{75}$ adalah $\frac{2}{5}$

Mengubah Bentuk Pecahan

Pecahan memiliki beberapa bentuk yaitu pecahan biasa, campuran, desimal, dan persen. Bentuk pecahan dapat diubah ke dalam bentuk lain. 

Cara mengubah bentuk pecahan antara lain :

✓ Mengubah pecahan biasa menjadi pecahan desimal. Caranya, ubah menjadi pecahan senilai dengan penyebut 10, 100, atau 1.000, dan seterusnya.

Contoh :

$\frac{1}{5}$ = $\frac{2}{10}$ = 0,2

✓ Mengubah pecahan biasa menjadi persen. Caranya, ubah menjadi pecahan senilai dengan penyebut 100, kemudian ubah menjadi persen.

Contoh :

$\frac{3}{4}$ = $\frac{75}{100}$ = 75%

✓ Mengubah pecahan desimal menjadi persen. Caranya, kalikan pecahan desimal tersebut dengan 100%.

Contoh :

0,5 × 100% = 50%

Mengurutkan Berbagai Bentuk Pecahan

Mengurutkan berbagai bentuk pecahan dapat dilakukan dengan menyamakan jenis semua pecahan terlebih dahulu, misalnya menjadi pecahan biasa, desimal, atau persen. Jika diubah ke bentuk pecahan biasa, samakan penyebutnya dan urutkan sesuai pembilangnya. Demikian juga dengan desimal dan persen. Caranya sama seperti mengurutkan bilangan bulat, yaitu dengan memperhatikan nilai tempatnya.

Contoh :

1,5; $\frac{7}{4}$; $\frac{8}{5}$; 125%; 1$\frac{2}{5}$

Urutkan pecahan-pecahan di atas dari yang terbesar !

Jawaban :

Samakan jenis pecahan terlebih dahulu, misalnya menjadi pecahan desimal.

1,5 (tetap)

$\frac{7}{4}$ = $\frac{7 × 25}{4 × 25}$ = $\frac{175}{100}$ = 1,75

$\frac{8}{5}$ = $\frac{8 × 2}{5 × 2}$ = $\frac{16}{10}$ = 1,6

125% = $\frac{125}{100}$ = 1,25

1$\frac{2}{5}$ = $\frac{7}{5}$ = $\frac{7 × 2}{5 × 2}$ = $\frac{14}{10}$ = 1,4

Urutan pecahan dari yang terbesar adalah 1,75; 1,6; 1,5; 1,4; 1,25

Jadi, urutan pecahan dari yang terbesar adalah $\frac{7}{4}$; $\frac{8}{5}$; 1,5; 1$\frac{2}{5}$; 125%

Itulah penjelasan materi soal pecahan kelas 6 kurikulum 2013. Bagaimana? Sudah siapkah kalian mengerjakan soal online matematika tentang pecahan?

Soal online ini sudah dilengkapi dengan pembahasan. Kalian bisa langsung mengklik kotak untuk membuka atau menutup pembahasan. Untuk melanjutkan soal berikutnya, minimal kalian harus mendapatkan skor 70. Jika belum berhasil mendapatkan skor minimal, silahkan refresh halaman untuk menjawab ulang.

Soal Pecahan Kelas 6 K13

Soal nomor 1
Bentuk pecahan paling sederhana dari  $\frac{20}{36}$ adalah ....
$\frac{10}{18}$
$\frac{7}{9}$
$\frac{5}{9}$
$\frac{5}{12}$

Pecahan paling sederhana dari $\frac{20}{36}$ = $\frac{\textrm{20 : 4}}{\textrm{36 : 4}}$ = $\frac{5}{9}$

Soal nomor 2
Pecahan paling sederhana dari  $\frac{75}{165}$ adalah ....
$\frac{3}{7}$
$\frac{3}{11}$
$\frac{5}{11}$
$\frac{5}{13}$

Pecahan paling sederhana dari $\frac{75}{165}$ = $\frac{\textrm{75 : 15}}{\textrm{165 : 15}}$ = $\frac{5}{11}$

Soal nomor 3
Perhatikan gambar berikut !

Pecahan paling sederhana berdasarkan gambar tersebut adalah ....
$\frac{4}{5}$
$\frac{1}{4}$
$\frac{13}{20}$
$\frac{17}{25}$

Pecahan yang ditunjukkan gambar adalah $\frac{68}{100}$ sehingga nilai pecahan paling sederhananya adalah $\frac{68}{100}$ = $\frac{\textrm{68 : 4}}{\textrm{100 : 4}}$ = $\frac{17}{25}$

Soal nomor 4
Bentuk pecahan paling sederhana dari  $\frac{81}{171}$ adalah ......
$\frac{9}{17}$
$\frac{9}{19}$
$\frac{7}{17}$
$\frac{9}{21}$

Pecahan paling sederhana dari $\frac{81}{171}$ = $\frac{\textrm{81 : 9}}{\textrm{171 : 9}}$ = $\frac{9}{19}$

Soal nomor 5
Bentuk pecahan paling sederhana dari $\frac{72}{152}$ adalah ....
$\frac{7}{9}$
$\frac{9}{19}$
$\frac{3}{28}$
$\frac{4}{29}$

Pecahan paling sederhana dari $\frac{72}{152}$ = $\frac{\textrm{72 : 8}}{\textrm{152 : 8}}$ = $\frac{9}{19}$

Soal nomor 6
Bentuk persen dari 0,87 adalah ....
0,87%
8,7%
87%
870%

0,87 = $\frac{87}{100}$ = 87%

Soal nomor 7
Bentuk desimal dari 17,5% adalah ....
0,175
1,75
17,5
175

17,5% = $\frac{17,5}{100}$ = $\frac{175}{1000}$ = 0,175
Jadi, bentuk desimal dari 17,5% adalah 0,175

Soal nomor 8
Bentuk persen dari $\frac{9}{25}$ adalah ....
36%
45%
48%
54%

$\frac{9}{25}$ = $\frac{36}{100}$ = 36%

Soal nomor 9
Pecahan desimal dari $\frac{19}{200}$ adalah ....
9,05
9,5
0,95
0,095

$\frac{19}{200}$ = $\frac{95}{1000}$ = 0,095

Soal nomor 10
Bentuk pecahan biasa dari 37$\frac{1}{2}$% adalah ....
$\frac{375}{1000}$
$\frac{375}{100}$
$\frac{375}{10}$
$\frac{37,5}{100}$

37$\frac{1}{2}$% = $\frac{37,5}{100}$ = $\frac{375}{1000}$

Soal nomor 11
Bentuk desimal dari 1 $\frac{7}{20}$ adalah ....
1,27
1,3
1,35
1,4

1$\frac{7}{20}$ = $\frac{27}{20}$ = $\frac{135}{100}$ = 1,35

Soal nomor 12
Bentuk pecahan biasa dari 0,725 adalah ....
$\frac{725}{10}$
$\frac{725}{100}$
$\frac{725}{1000}$
$\frac{725}{10000}$

0,725 = $\frac{725}{1000}$

Soal nomor 13
Bentuk pecahan campuran paling sederhana dari $\frac{475}{225}$ adalah ....
2$\frac{1}{7}$
2$\frac{3}{7}$
2$\frac{1}{9}$
2$\frac{3}{5}$

$\frac{475}{225}$ = $\frac{\textrm{475 : 25}}{\textrm{225 : 25}}$ = $\frac{19}{9}$ = 2$\frac{1}{9}$

Soal nomor 14
Bentuk persen dari pecahan 1$\frac{3}{50}$ adalah ....
106%
108%
109%
112%

1$\frac{3}{50}$ = $\frac{1 × 50 + 3}{50}$ = $\frac{53}{50}$ = $\frac{106}{100}$ = 106%

Soal nomor 15
Bentuk pecahan desimal dari $\frac{3}{8}$ adalah ....
0,325
0,375
0,425
0,475

$\frac{3}{8}$ = $\frac{3 × 125}{8 × 125}$ = $\frac{375}{1000}$ = 0,375

Soal nomor 16
Bentuk persen dari 3$\frac{4}{5}$ adalah ....
345%
360%
380%
385%

3$\frac{4}{5}$ = $\frac{3 × 5 + 4}{5}$ = $\frac{19}{5}$ = $\frac{380}{100}$ = 380%

Soal nomor 17
Bentuk pecahan biasa dari 1,2% adalah ....
$\frac{12}{10}$
$\frac{12}{100}$
$\frac{12}{1000}$
$\frac{1,2}{100}$

1,2% = $\frac{1,2 × 10}{100 × 10}$ = $\frac{12}{1000}$

Soal nomor 18
Perhatikan pecahan-pecahan berikut!
1,35; 156%; $\frac{7}{4}$; 1$\frac{3}{5}$

Urutan pecahan dari yang terbesar adalah ....
$\frac{7}{4}$; 1,35; 156%; 1$\frac{3}{5}$
156%; $\frac{7}{4}$; 1$\frac{3}{5}$; 1,35
1$\frac{3}{5}$; 1,35; 156%; $\frac{7}{4}$
$\frac{7}{4}$; 1$\frac{3}{5}$; 156%; 1,35

1,35; 156%; $\frac{7}{4}$; 1$\frac{3}{5}$
Ubah bentuk pecahan menjadi pecahan desimal
1,35 (tetap)
156% = $\frac{156}{100}$ = 1,56
$\frac{7}{4}$ = $\frac{175}{100}$ = 1,75
1$\frac{3}{5}$ = $\frac{8}{5}$ = $\frac{16}{10}$ = 1,6
Urutan pecahan dari yang terbesar adalah 1,75; 1,6; 1,56; 1,35
Jadi, urutan pecahan dari yang terbesar adalah $\frac{7}{4}$; 1$\frac{3}{5}$; 156%; 1,35

Soal nomor 19
Perhatikan pecahan-pecahan berikut!
$\frac{3}{4}$; 0,55; 53%; $\frac{4}{5}$
Urutan pecahan dari yang terkecil adalah ....
53%; 0,55; $\frac{3}{4}$; $\frac{4}{5}$
53%; $\frac{3}{4}$; 0,55; $\frac{4}{5}$
53%; 0,55; $\frac{4}{5}$; $\frac{3}{4}$
$\frac{3}{4}; $53%; 0,55; $\frac{4}{5}$

$\frac{3}{4}$; 0,55; 53%; $\frac{4}{5}$
Ubah bentuk pecahan menjadi pecahan desimal
$\frac{3}{4}$ = $\frac{75}{100}$ = 0,75
0,55 (tetap)
53% = $\frac{53}{100}$ = 0,53
$\frac{4}{5}$ = $\frac{8}{10}$ = 0,8
Urutan pecahan dari yang terkecil adalah 0,53; 0,55; 0,75; 0,8
Jadi, urutan pecahan dari yang terkecil adalah 53%; 0,55; $\frac{3}{4}$; $\frac{4}{5}$

Soal nomor 20
Perhatikan pecahan-pecahan berikut!
65%; $\frac{11}{20}$; 0,825; $\frac{19}{50}$; $\frac{5}{8}$
Urutan pecahan dari yang terbesar adalah ....
0,825; $\frac{5}{8}$; 65%; $\frac{11}{20}$; $\frac{19}{50}$
0,825; 65%; $\frac{5}{8}$; $\frac{11}{20}$; $\frac{19}{50}$
$\frac{5}{8}$; 65%; $\frac{11}{20}$; 0,825; $\frac{19}{50}$
$\frac{19}{50}$; 65%; $\frac{11}{20}$; 0,825; $\frac{5}{8}$

65%; $\frac{11}{20}$; 0,825; $\frac{19}{50}$; $\frac{5}{8}$
Ubah bentuk pecahan menjadi pecahan desimal
65% = $\frac{65}{100}$ = 0,65
$\frac{11}{20}$ = $\frac{55}{100}$ = 0,55
0,825 (tetap)
$\frac{19}{50}$ = $\frac{36}{100}$ = 0,36
$\frac{5}{8}$ = $\frac{625}{1000}$ = 0,625
Urutan pecahan dari yang terbesar adalah 0,825; 0,65; 0,625; 0,55; 0,36
Jadi, urutan pecahan dari yang terbesar adalah 0,825; 65%; $\frac{5}{8}$; $\frac{11}{20}$; $\frac{19}{50}$

Javascript pada browser perlu diaktifkan untuk menampilkan soal online ini. Jika soal online tidak berjalan, kalian dapat mengunjungi Soal Pecahan Kelas 6 Kurikulum 2013

Read More

Bagikan Artikel ini

Mengenal Lingkaran, Unsur-unsur, Rumus, dan Contoh Soal

Ada beberapa materi pelajaran matematika untuk kelas 6 kurikulum 2013 yang harus kita pelajari salah satunya adalah Lingkaran. Kali ini saya akan membahas materi tersebut secara rinci. Materi pokok tentang lingkaran adalah Mengenal Lingkaran, Unsur-unsur Lingkaran, Rumus Lingkaran, dan Contoh Soal Lingkaran. 

Mengenal Lingkaran 

Lingkaran adalah garis lengkung yang bertemu kedua ujungnya dan semua titik yang terletak pada garis lengkung tersebut jaraknya sama terhadap titik tertentu dalam lingkaran itu. Titik tertentu tersebut dinamakan titik pusat dan jarak yang sama tersebut dinamakan jari-jari. 

Lingkaran tidak selalu merupakan bangun datar yang memiliki bidang. Contohnya benda-benda di sekitar kita yang bentuknya tidak mutlak bangun datar lingkaran dua dimensi.

Jika lingkaran bukan merupakan bangun datar dua dimensi, bisa saja lingkaran tersebut berupa lengkungan yang bertemu kedua ujungnya dan titik-titik yang membentuk lengkungan tersebut memiliki panjang yang sama pada titik pusat lingkaran. 

Dan jika lingkaran merupakan bangun datar dua dimensi, maka lengkungan pada lingkaran itu saling berkaitan serta mengelilingi titik pusat dan juga membentuk daerah di dalamnya.

Unsur-unsur Lingkaran

Lingkaran memiliki bagian-bagian yang menyusunnya. Bagian-bagian tersebut adalah unsur-unsur lingkaran. Untuk lebih jelasnya perhatikan gambar berikut !

1. Titik Pusat Lingkaran

Lingkaran memiliki sebuah titik yang terletak tepat di tengah lingkaran. Titik ini adalah pusat lingkaran. Titik pusat lingkaran mempunyai jarak yang sama dengan semua titik pada tepi lingkaran. Pada gambar, titik O disebut titik pusat lingkaran.

2. Jari-Jari Lingkaran

Jari-jari lingkaran (r) adalah jarak antara pusat lingkaran dengan sembarang titik pada tepi lingkaran. Pada gambar, AO, BO, dan CO disebut jari-jari lingkaran. Panjang AO = BO = CO 

3. Diameter Lingkaran

Diameter (d) adalah garis yang menghubungkan dua titik pada tepi lingkaran dengan melalui titik pusat. Diameter disebut juga gans tengah lingkaran. Pada gambar, garis AB disebut diameter lingkaran. Panjang diameter sama dengan dua kali jari-jari lingkaran.

AB = 2 x AO 

AB = 2 x BO

AB = 2 x CO

d = 2r

4. Busur Lingkaran

Busur lingkaran adalah garis berbentuk lengkung pada tepian lingkaran. Pada gambar, garis lengkung AC disebut busur lingkaran. Busur lingkaran merupakan potongan dari keliling lingkaran. Busur lingkaran dilambangkan dengan $\frown$.

5. Tali Busur Lingkaran

Tali busur lingkaran adalah garis yang menghubungkan dua titik pada lingkaran tanpa melalui titik pusat. Pada gambar, gans AC disebut tali busur.

6. Apotema

Apotema adalah garis tegak lurus pada tali busur yang merupakan jarak terpendek antara tali busur dengan titik pusat. Pada gambar, OD disebut apotema.

7. Juring Lingkaran

Juring lingkaran adalah daerah yang dibatasi oleh busur dan dua jari-jari lingkaran  Juring lingkáran merupakan bagian dari luas lingkaran. Pada gambar, daerah yang diarsir OBC disebut juring OBC.

8. Tembereng

Tembereng adalah daerah yang dibatasi oleh busur dan tali busur. Tembereng bentuknya mirip dengan lambung kapal. Pada gambar, daerah berwarna biru AC disebut tembereng.

Rumus Keliling Lingkaran

Keliling lingkaran adalah panjang lengkungan pembentuk lingkaran. Keliling lingkaran dapat dihitung jika diketahui jari-jarinya (r) atau diameternya (d). Pada lingkaran terdapat nilai yang sama untuk perbandingan keliling dan diameter. Nilai tersebut adalah $\frac{22}{7}$ atau 3,14. Nilai tersebut dinamakan $\pi $ (phi).

Nilai phi $\frac{22}{7}$ digunakan jika diameter atau jari-jari lingkaran dapat dibagi 7. Nilai phi 3,14 digunakan jika diameter atau jari-jari lingkaran tidak dapat dibagi 7. 

Cara menghitung keliling lingkaran jika diketahui jari-jari

Contoh soal 

Sebuah lingkaran berjari-jari 14 cm, keliling dari lingkaran tersebut adalah ....

Pembahasan:

r = 14 cm

K = 2 x $\pi $ x r

K = 2 x $\frac{22}{7}$ x 14

K = 88 cm

Contoh soal 

Sebuah lingkaran berjari-jari 5 cm, keliling dari lingkaran tersebut adalah ....

Pembahasan:

r = 5 cm

K = 2 x $\pi $ x r

K = 2 x 3,14 x 5

K = 31,4 cm

Cara menghitung keliling lingkaran jika diketahui diameter

Contoh soal 

Sebuah lingkaran berdiameter 14 cm, keliling dari lingkaran tersebut adalah ....

Pembahasan

d = 14 cm

K = $\pi $ x d

K = $\frac{22}{7}$ x 14

K = 44 cm

Contoh soal 

Sebuah lingkaran berdiameter 5 cm, keliling dari lingkaran tersebut adalah ....

Pembahasan:

d = 5 cm

K = $\pi $ x d

K = 3,14 x 5

K = 15,7 cm

Cara menghitung jari-jari lingkaran jika diketahui kelilingnya

Contoh soal

Diketahui panjang keliling lingkaran 176 cm. Panjang jari-jari lingkaran tersebut adalah ....

Pembahasan:

K = 176 cm

r = $\frac{K}{2\pi } $ 

r = $\frac{176}{2\times \frac{22}{7}} $ = $\frac{176}{ \frac{44}{7}} $ = 176 x $\frac{7}{44 } $ = 28

r = 28 cm

Rumus Luas Lingkaran

Luas lingkaran adalah daerah yang dibatasi oleh lingkaran tersebut. Luas lingkaran dapat dihitung dengan menggunakan jari-jari lingkaran. Jika yang diketahui diameternya, maka diameter harus diubah dulu menjadi jari-jari. Caranya, diameter dibagi 2.

Cara menghitung luas lingkaran jika diketahui jari-jari

Contoh soal 

Sebuah lingkaran memiliki jari-jari 7 cm, luas dari lingkaran tersebut adalah ....

Pembahasan

r = 7 cm

L = $\pi $ x $r^{2}$

L = $\frac{22}{7}\times 7 \times 7$

L = 154 cm²

Cara menghitung jari-jari lingkaran jika diketahui luasnya

Contoh soal 

Sebuah lingkaran memiliki luas 616 cm². Jari-jari dari lingkaran tersebut adalah ....

Pembahasan

L = 616 cm²

r = $\sqrt{\frac{L}{\pi}}$

r = $\sqrt{\frac{616}{\frac{22}{7}}}$

r = $\sqrt{616 \times \frac{7}{22}}$

r = $\sqrt{196}$

r = 14 cm

Rumus Mencari Panjang Apotema

Keterangan:

a = apotema

r = jari-jari

tb = tali busur

Panjang tali busur dan apotema berhubungan dengan jari-jari. Cara mencari panjang apotema lingkaran yang diketahui jari-jari dan panjang tali busurnya adalah dengan menggunakan rumus pythagoras yaitu akar pangkat dua dari kuadrat jari-jari dikurangi dengan kuadrat setengah panjang tali busur.

Contoh soal

Sebuah lingkaran memiliki panjang tali busur 16 cm dan jari-jari 10 cm. Panjang apotema yang terbentuk adalah ....

Pembahasan

r = 10 cm

tb = 16 cm = ½ tb = 8 cm

a = $\sqrt{r^{2} - \left ( \frac{1}{2} tb\right )^{2}}$ cm

a = $\sqrt{10^{2} - 8^{2}}$ cm

a = $\sqrt{100 - 64}$ cm

a = $\sqrt{36}$ cm

a = 6 cm

Klik di bawah ini untuk mendapatkan Soal yang lebih banyak tentang Lingkaran ⇩

Soal Keliling dan Luas Lingkaran

Soal Online Lingkaran 1

Soal Online Lingkaran 2

Demikianlah artikel tentang Mengenal Lingkaran, Unsur-unsur, Rumus, dan Contoh Soal. Semoga bermanfaat dan dapat menambah wawasan untuk kita semua.

Read More

Bagikan Artikel ini

Soal Lingkaran Kelas 6 Kurikulum 2013 dan Kunci Jawaban

Halo adik-adik kelas 6, berikut ini kakak admin bagikan Soal Lingkaran. Ada 20 soal tentang lingkaran yang materinya meliputi definisi lingkaran, unsur-unsur lingkaran, dan rumus lingkaran. 

Sebelum mengerjakan, kalian bisa mempelajari materi tentang lingkaran. Apa yang dimaksud dengan lingkaran? Apa saja unsur-unsur lingkaran? Rumus-rumus lingkaran yang harus dihafalkan apa saja. Dan cara mengerjakan soal lingkaran itu bagaimana bisa kalian klik tulisan di bawah ini ya. 

Mengenal Lingkaran, Unsur-unsur Lingkaran, Rumus Lingkaran, dan Contoh Soal

Seperti soal-soal sebelumnya, Soal Lingkaran ini berupa kuis atau tes online yang mana kalian bisa langsung menjawab soal dengan cara mengklik bulatan di depan jawaban yang kalian anggap paling benar. 

Setelah mengerjakan soal, kalian dapat melihat langsung hasilnya secara online yaitu skor yang ditampilkan otomatis. Jika jawaban kalian benar maka skor otomatis bertambah. Namun jika jawaban kalian salah, jangan khawatir karena skor tidak akan berkurang. Skor untuk satu soal adalah 5. Total skor jika semua jawaban benar adalah 100. Selamat mengerjakan ....

Soal Lingkaran Kelas 6
Petunjuk: klik lingkaran yang ada di depan jawaban yang benar. Poin untuk satu soal adalah 5

---

1. Kurva tertutup sederhana yang merupakan tempat kedudukan titik-titik yang berjarak sama terhadap suatu titik tertentu disebut ....
juring
lingkaran
jari-jari
tembereng

2. Pernyataan berikut yang benar adalah ....
diameter bukan merupakan tali busur
juring adalah daerah pada lingkaran yang dibatasi oleh dua jari-jari dan sebuah busur
juring merupakan bagian dari tembereng 
apotema sama dengan jari-jari

3. Garis yang menghubungkan dua titik pada keliling lingkaran dan melalui pusat lingkaran disebut ....
jari-jari
tali busur
diameter
apotema

4. Garis yang menghubungkan titik pusat lingkaran dengan tali busur lingkaran disebut ....
jari-jari
diameter
apotema
juring

5. Panjang seluruh lengkung lingkaran disebut ....
jari-jari
diameter
tali busur
keliling lingkaran

6. Tali busur terpanjang dari sebuah lingkaran adalah ....
diameter
apotema
jari-jari 
juring

7. Unsur lingkaran berupa garis lurus yang menghubungkan dua titik sembarang di sepanjang lengkungan lingkaran disebut ....
juring
tembereng
busur
tali busur

8. Perhatikan gambar berikut !

Pada gambar di atas, daerah yang diarsir disebut ....
busur
tali busur
juring
tembereng

9. Perhatikan gambar berikut !

Pada gambar di atas, garis AB disebut ....
tali busur
apotema
diameter
jari-jari

10. Perhatikan gambar berikut !

Daerah yang diarsir disebut ....
juring
busur
tali busur
tembereng

11. Perhatikan gambar berikut !

Apotema ditunjukkan oleh garis ....
OA
AC
OE
OB

12. Perhatikan gambar berikut !

Garis lengkung dari A ke C disebut ....
busur
diameter
tali busur
apotema

13. Garis lurus yang menghubungkan titik pusat lingkaran dengan satu titik pada keliling lingkaran disebut ....
apotema
diameter
tali busur
jari-jari

14. Jari-jari lingkaran diperoleh dari ....
r = 2d
r = 3d
r = $ \frac{1}{2}$d
r = 4d

15. Jari-jari lingkaran yang berpusat di O adalah 6 cm. Diameter lingkaran tersebut adalah .... cm.
10
12
14
16

16. Diameter lingkaran yang jari-jarinya 7 cm adalah .... cm.
12
14
16
18

17. Sebuah lingkaran dengan diameter 20 cm. Jari-jari lingkaran tersebut adalah .... cm.
5
10
15
40

18. Panjang apotema pada lingkaran yang memiliki jari-jari 13 cm dan panjang tali busur 10 cm adalah .... cm.
9
10
11
12

19. Sebuah lingkaran mempunyai diameter 16 cm. Jari-jari lingkaran tersebut adalah .... cm.
4
6
8
32

20. Jika sebuah lingkaran diketahui jari-jari p, diameter q, keliling K, dan luas L, maka rumus yang benar di bawah ini adalah ....
L = 2$\pi $p 
K = $\pi $q
L = $\pi $q²
K = $\pi $r²

Bagaimana kuisnya? Sudah dapat skor 100 belum? Kalau belum, silahkan   COBA LAGI

Javascript pada browser perlu diaktifkan untuk menampilkan soal online ini. Jika soal online tidak berjalan, kalian dapat mengunjungi Soal Lingkaran Kelas 6 Kurikulum 2013

Jika ingin mendapatkan lebih banyak contoh soal bangun datar lingkaran, silahkan buka link di bawah ini ⇩

Soal Luas dan Keliling Lingkaran plus Kunci Jawaban

Itulah Soal Lingkaran Kelas 6 Kurikulum 2013 dan Kunci Jawaban. Semoga bermanfaat untuk kita semua.

Read More

Bagikan Artikel ini

Soal Cerita Matematika Operasi Hitung Campuran

Berikut ini adalah Soal Cerita Matematika Operasi Hitung Campuran berupa kuis yang mana kalian bisa langsung menjawab soal dengan cara mengklik bulatan di depan jawaban yang kalian anggap paling benar. Jika jawaban kamu benar atau salah pun, skor akan langsung ditampilkan otomatis. Skor untuk satu soal adalah 5. Total skor jika semua jawaban benar adalah 100. 

Soal online ini sudah dilengkapi dengan pembahasan. Kamu bisa langsung mengklik kotak untuk  membuka atau menutup pembahasan. Untuk melanjutkan soal berikutnya, minimal kamu harus mendapatkan skor 70. Jika belum berhasil mendapatkan skor minimal, maka kamu bisa merefresh halaman untuk menjawab ulang. 

Bagaimana? Sudah siapkah kamu mengerjakan? Dengan adanya soal online ini, tentunya pembelajaran menjadi lebih bervariasi. Ayo uji kemampuan kamu dan dapatkan nilai sempurna !

Soal Cerita Matematika Operasi Hitung Campuran

Soal nomor 1
Sania memperoleh bingkisan sebanyak 30 kotak berisi permen. Setiap kotak berisi 10 permen. Sania mengambil 30 permen untuk dirinya sendiri, dan sisanya diberikan kepada 30 temannya dengan sama banyak. Banyak permen yang diterima setiap teman Sania adalah ....
6
7
8
9

{(30 × 10) - 30} : 30 = 9
Jadi, setiap teman menerima 9 permen

Soal nomor 2
Pak Made mempunyai 10 buah jeruk dan 5 keranjang jeruk. Setiap keranjang berisi 20 buah jeruk. Jika jeruk itu diberikan sama banyak kepada 5 orang, maka setiap orang menerima .... buah.
44
20
22
24

{10 + (5 × 20)} : 5 = 22
Jadi, setiap orang menerima 22 buah jeruk

Soal nomor 3
Nura mendapat hadiah dari tantenya berupa 10 kotak permen. Setiap kotaknya terdiri atas 20 permen. Nura mengambil 32 permen untuk dirinya sendiri dan sisanya dibagikan kepada 24 temannya dengan jumlah sama banyak. Banyak permen yang didapatkan setiap teman Nura adalah ....
5
6
7
8

(10 × 20 - 32) : 24 = 7
Jadi, banyak permen yang didapatkan teman Nura adalah 7

Soal nomor 4
Andi memiliki koleksi komik sebanyak 24 seri. Sebanyak 9 seri terdiri dari 9 judul  dan 15 seri terdiri dari 12 judul. Andi sudah membaca komik tersebut sebanyak 211 judul. Sisa komik yang belum dibaca Andi adalah .... judul.
45
50
55
61

{(9 × 9) + (15 × 12)} - 211 = 50
Jadi, sisa komik yang belum dibaca Andi sebanyak 50 judul

Soal nomor 5
Di toko tersedia 12 karung beras. Setiap karung beras beratnya 40 kg. Jika hari ini beras laku 175 kg, maka sisa beras adalah .... kg.
305
310
315
320

12 × 40 - 175 = 305
Jadi, sisa beras ada 305 kg

Soal nomor 6
Seorang pedagang memiliki 5 peti telur. Berat telur dalam setiap peti 16 kg. 1 kg telur berjumlah 16 butir. Kemudian, dari setiap peti diambil masing-masing 3 kg telur. Jumlah telur dari kelima peti sekarang adalah ....
1.020
1.026
1.034
1.040

{5 × (16 × 16)} - {5 × (3 × 16)} = 1.280 - 240 = 1.040
Jadi, jumlah telur dari kelima peti sekarang adalah 1.040 butir

Soal nomor 7
Bibi membuat 200 roti kukus. Kemudian,  bibi membuat lagi 50 roti kukus.  Selanjutnya, semua roti kukus tersebut akan dibagikan kepada 4 orang pelanggannya dengan bagian yang sama. Jumlah roti kukus yang diterima setiap pelanggan bibi adalah ....
40
45
50
55

(200 + 50) : 4 = 50
Jadi, jumlah roti kukus yang diterima setiap pelanggan bibi adalah 50 buah

Soal nomor 8
Seno menyimpan kelereng miliknya dalam 5 kaleng. Setiap kalengnya berisi 15 butir kelereng. Kemudian, Seno memberikan 55 butir kelereng kepada temannya. Setelah itu, Budi datang memberikan 2 kaleng masing-masing berisi 25 butir kelereng kepada Seno. Jumlah kelereng yang dimiliki Seno sekarang adalah ....
65
70
75
80

(5 × 15 - 55) + (2 × 25) = 20 + 50 = 70
Jadi, kelereng yang dimikiki Seno sekarang adalah 70 butir

Soal nomor 9
Ibu membeli 6 kardus apel dan mendapat bonus 10 buah apel. Setiap kardus berisi 32 apel. Apel tersebut dikemas kembali menggunakan 8 kantong plastik. Setiap kantong berisi 12 buah apel. Banyak apel yang belum dikemas adalah ....
102
106
108
110

(6 × 32 + 10) - (8 × 12) = 202 - 96 = 106
Jadi, banyak apel yang belum dikemas adalah 106 buah

Soal nomor 10
Ibu mempunyai 3 liter sirup nanas. Sirup tersebut akan dituangkan pada gelas dengan volume 600 mililiter. Banyak gelas yang dibutuhkan ibu adalah ....
2
3
5
6

3 liter = 3.000 mililiter
3.000 : 600 = 5
Jadi, banyak gelas yang dibutuhkan ibu adalah 5

Soal nomor 11
Bu Ratna membeli 150 kantong beras. Setiap kantong berisi 5 kg beras. Sebanyak 15 kg diberikan kepada nenek. Beras yang masih tersisa dibagikan kepada 49 tetangga. Masing-masing tetangga menerima beras .... kg.
12
13
15
17

(150 × 5 - 15) : 49 = 15
Jadi, masing-masing tetangga menerima 15 kg beras

Soal nomor 12
Hari ini paman memanen 192 buah mangga dan 7 keranjang buah apel. Mangga-mangga tersebut dimasukkan ke dalam beberapa keranjang. Tiap keranjang berisi 24 buah mangga. Banyak semua keranjang mangga dan apel paman adalah ....
12
14
15
18

192 : 24 + 7 = 8 + 7 = 15
Jadi, banyak swmua keranjang apel dan mangga adalah 15

Soal nomor 13
Hasil kebun mangga Pak Harun ada 12 keranjang. Setiap keranjang berisi 192 buah mangga. Pak Harun akan menjual mangga tersebut kepada 8 pedagang secara merata. Setiap pedagang akan memperoleh .... buah mangga.
288
290
292
296

12 × 192 : 8 = 288
Jadi, setiap pelanggan akan memperoleh 288 buah mangga

Soal nomor 14
Sebuah gedung pertunjukan dapat menampung 550 orang yang terdiri atas 400 orang kelas ekonomi dan sisanya kelas utama. Harga tiket kelas ekonomi Rp 5.000,00, sedangkan kelas utama Rp 10.000,00. Jika gedung itu penuh, uang yang diperoleh dari penjualan tiket tersebut adalah ....
Rp 3.200.000,00
Rp 3.500.000,00
Rp 3.700.000,00
Rp 4.000.000,00

Kapasitas gedung = 550 orang
Kelas ekonomi = 400
Kelas utama = 150 orang
(400 × 5.000) + (150 × 10.000) = 2.000.000 + 1.500.000 = 3.500.000
Jadi, uang yang diperoleh dari penjualan tiket jika gedung itu penuh adalah Rp 3.500.000,00

Soal nomor 15
Desa Sugihwaras menerima 738 kantong beras raskin. Setiap kantong berisi 24 kg. Beras itu akan dikirim ke 9 RW dengan jatah yang sama. Setiap RW akan menerima .... kg.
1.966
1.968
1.972
1.978

738 × 24 : 9 = 1.968
Jadi, setiap RW akan menerima 1.968 kg

Soal nomor 16
Arman memiliki pensil sebanyak 12 kotak. Setiap kotak berisi 36 pensil. Pada hari ulang tahunnya, ia membagikan semua pensilnya sama banyak kepada 27 temannya. Banyak pensil yang diterima setiap teman adalah .... batang.
14
16
18
20

12 × 36 : 27 = 16
Jadi, banyak pensil yang diterima setiap teman adalah 16 batang

Soal nomor 17
Pak Rudi memiliki 8 pak buku. Setiap pak isinya 12 buku. Pak Anton memiliki 12 pak buku. Setiap pak isinya 20 buku. Seluruh buku tersebut dibagikan oleh Pak Rudi dan Pak Anton kepada 16 siswanya dengan sama banyak. Setiap siswa akan mendapatkan buku sebanyak = .... buah.
16
17
18
21

(8 × 12 + 12 × 20) : 16 = 21
Jadi, setiap siswa akan mendapatkan buku sebanyak 21 buah

Soal nomor 18
Pak Widi memiliki 120 kantong beras. setiap kantongnya berisi beras 5 kg. Sebanyak 40 kg diberikan kepada adiknya Bu Widi, sisanya dibagikan kepada 40 keluarga miskin dengan sama banyak. Masing-masing akan mendapatkan beras .... kg. 
12
13
14
15

(120 × 5 - 40) : 40 = 14
Jadi, masing-masing akan mendapatkan beras 14 kg

Soal nomor 19
Dita memiliki manik-manik yang disimpan dalam 24 kaleng. Setiap kaleng berisi 132 butir manik-manik. Oleh karena kalengnya rusak, Dita ingin memindahkan semua manik-maniknya ke dalam 8 kaleng yang baru. Banyak manik-manik yang ada di setiap kaleng yang baru adalah ....
44
396
1.032
3.160

24 × 132 : 8 = 396
Jadi, banyak manik-manik yang ada di setiap kaleng yang baru adalah 396

Soal nomor 20
Seluruh peserta diklat akan disediakan 60 kamar hotel. Setiap kamar dihuni oleh 2 orang. Dalam pembagian tugas, panitia akan membagi menjadi 12 kelompok. Setiap kelompok terdiri atas .... orang.
10
36
42
46

60 × 2 : 12 = 10
Jadi, setiap kelompok terdiri atas 10 orang

Read More

Bagikan Artikel ini

Soal Operasi Hitung Campuran dan Pembahasan

Berikut ini adalah Soal Matematika Kelas 6 Operasi Hitung Campuran berupa kuis yang mana kalian bisa langsung menjawab soal dengan cara mengklik bulatan di depan jawaban yang kalian anggap paling benar. Jika jawaban kamu benar atau salah pun, skor akan langsung ditampilkan otomatis. Skor untuk satu soal adalah 5. Total skor jika semua jawaban benar adalah 100. 

Soal online ini sudah dilengkapi dengan pembahasan. Kamu bisa langsung mengklik kotak untuk  membuka atau menutup pembahasan. Untuk melanjutkan soal berikutnya, minimal kamu harus mendapatkan skor 70. Jika belum berhasil mendapatkan skor minimal, maka kamu bisa merefresh halaman untuk menjawab ulang. 

Bagaimana? Sudah siapkah kamu mengerjakan? Dengan adanya soal online ini, tentunya pembelajaran menjadi lebih bervariasi. Ayo uji kemampuan kamu dan dapatkan nilai sempurna !

Soal Operasi Hitung Campuran

Soal nomor 1
Hasil dari 2.144 - 1.230 + 312 - 510 adalah ....
816
796
716
616

2.144 - 1.230 + 312 - 510 = 716

Soal nomor 2
Hasil dari 144 : 6 × 3 : 2 adalah = ....
4
8
18
36

144 : 6 × 3 : 2 = 24 × 3 : 2 = 72 : 2 = 36

Soal nomor 3
Hasil dari 22.453 + 17.512 - 16.129 + 24.268 adalah ....
49.104
2.196
578
568

23.453 + 17.512 - 16.129 + 24.268 = 49.104

Soal nomor 4
Hasil dari (52 × 12) : (13 × 6) adalah ....
14
12
8
6

(52 × 12) : (13 × 6) = 624 : 78 = 8

Soal nomor 5
Hasil dari 25 × 12 - 50 + 500 : 2 adalah ....
25
375
450
500

25 × 12 - 50 + 500 : 2 = 300 - 50 + 250 = 500

Soal nomor 6
Hasil dari 100 : (75 - 25) × 250 + 50 adalah ....
550
600
650
700

100 : (75 - 25) × 250 + 50 = 100 : 50 × 250 + 50 = 2 x 250 + 50 = 550

Soal nomor 7
Hasil dari 9.444 : 12 × 202 - 101.000 adalah ....
56.894
57.974
58.014
58.164

9.444 : 12 × 202 - 101.000 = 787 x 202 - 101.000 = 57.974

Soal nomor 8
Jika hasil dari 644 : (2 × 14) + (120 - 58) adalah ....
65
75
85
90

644 : (2 × 14) + (120 - 58) = 23 + 62 = 85

Soal nomor 9
Jika 60 + 300 : 30 x 5 = n, maka nilai n adalah ....
60
80
110
120

60 + 300 : 30 x 5 = 60 + 10 x 5 = 60 + 50 = 110

Soal nomor 10
Hasil dari (70 + 6) × 8 : 4 adalah ....
132
142
152
162

(70 + 6) × 8 : 4 = 76 x 8 : 4 = 152 : 4 = 152

Soal nomor 11
{56 - (30 : 5)} × {50 : (-5)} .... 
400
500
55
600

56 - (30 : 5)} × {50 : (-5)} = 56 - 6 × 10 = 50 × 10 = 500

Soal nomor 12
24 + 32 : {28 + (-24)}= ....
14
28
32
46

24 + 32 : {28 + (-24)} = 24 + 32 : 4 = 24 + 8 = 32

Soal nomor 13
(45 - 20) × {(28 × 2) : 7} = ....
150
180
200
240

(45 - 20) × {(28 × 2) : 7} = 25 × (56 : 7) = 25 × 8 = 200

Soal nomor 14
832 : (-32) × {228 + (-188) - 351} ....
-10.166
10.166
-10.557
10.557

832 : (-32) × {228 + (-188) - 351} = -26 × (-391) = 10.166

Soal nomor 15
Hasil dari (324 + (-352) × 45 : {-158 - (-186)} = ....
35
45
-45
-55

(324 + (-352) × 45 : {-158 - (-186)} = -28 x 45 : 28 = -45

Soal nomor 16
{-1.557 - (-2.357)} : 25 × {225 + (-230)} = ....
150
-150
150
-160

{-1.557 - (-2.357)} : 25 × {225 + (-230)} = 800 : 25 x (-5) = -160

Soal nomor 17
Diketahui 98 + 276 - 158 + 241 = ....
389
374
457
297

98 + 276 - 158 + 241 = 457

Soal nomor 18
Jika 21 + 4 × 5 = n, maka n adalah ....
40
41
120
125

21 + 4 × 5 = 21 + 20 = 41

Soal nomor 19
Hasil dari 160 - 12 × 13 + 210 adalah ....
214
213
212
211

160 - 12 × 13 + 210 = 160 - 156 + 210 = 214

Soal nomor 20
Hasil dari 1.750 + 1.500 : 30 - 1.250 adalah ....
530
540
550
560

1.750 + 1.500 : 30 - 1.250 = 1.750 + 50 - 1.250 = 550

Read More

Bagikan Artikel ini